The Dihedral Angle of a Pyramid Roof with Regular Polygon Base

When designing pyramid-shaped roofs one often needs the dihedral angle between adjacent roof facets. This article derives a compact formula for that dihedral angle $\theta$ in terms of the roof pitch $v$ (the angle between the base plane and a joist running from a base corner to the apex) for a pyramid with a regular $n$-gon base. The main result is a single closed form that covers any regular $n$.

Geometry setup

• The base is a regular polygon with $n$ vertices (corners).
• The apex is vertically above the center of the polygon; denote the vertical height by $h$.
• A joist runs from a base vertex to the apex and makes an angle $v$ with the base plane (the pitch).
• We seek the dihedral angle $\theta$ between two adjacent roof facets (the two triangular faces that meet along the roof ridge).

To analyze the geometry we use three helpful slices / views:

1. a vertical cross-section through a base vertex and the apex (shows the joist pitch $v$);
2. the vertical plane containing the angle bisector of a base vertex (this is the symmetry plane that contains the ridge);
3. the plan (top) view of the base polygon (to relate horizontal lengths by symmetry).

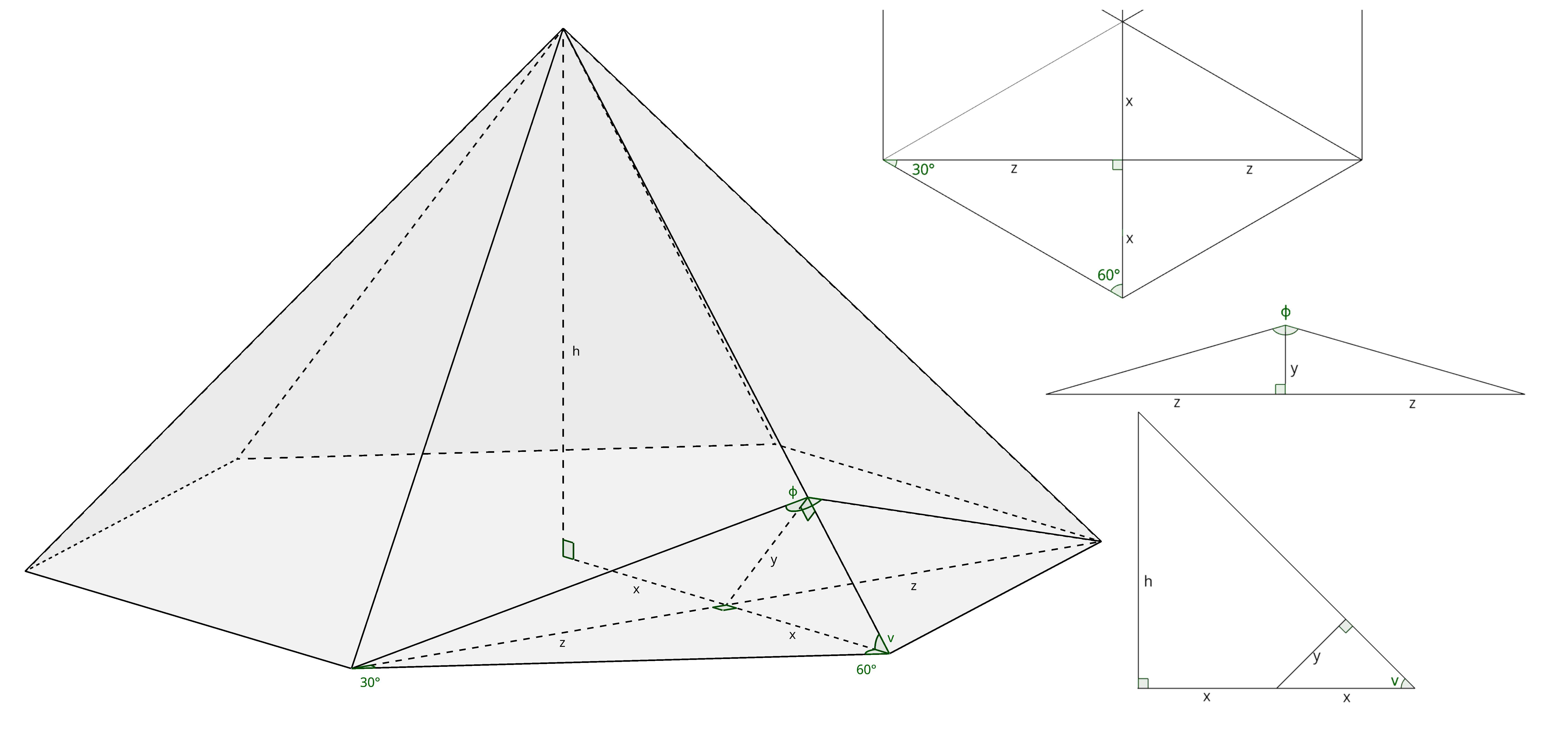
Symmetry: where the ridge lies

Because the base is regular and the apex lies above the center, the two triangular facets adjacent to any chosen base vertex are mirror images with respect to the vertical plane that contains the angle bisector of that base vertex. Consequently:

• the ridge (the line where those two facets meet) lies in that vertical bisector plane, and
• the projection of the ridge onto the base plane is the angle bisector of the chosen vertex.

A small even/odd nuance:

for even $n$ (e.g. $n=6$) the bisector passes through the opposite vertex; for odd $n$ it meets the midpoint of the opposite side. Either way, the ridge projects to the angle bisector, and the vertical plane through that bisector contains the ridge. This symmetry justifies the geometric decomposition used below.

Base plan geometry

Let the interior angle at each vertex of the regular $n$-gon be

$$\alpha =\pi -\frac{2\pi }{n}.$$

The angle bisector splits $\alpha$ into two equal angles $\frac{\alpha }{2}$. Consider the right triangle formed in the plan view by the bisector and the direction of an adjacent side: call the horizontal (plan) distances in that triangle $x$ and $z$ so that $z$ is the leg along the bisector direction and $x$ is the leg along (the projection of) the side direction. By simple trigonometry in the plan:

$$\frac{z}{x}=\tan \left(\frac{\alpha }{2}\right)=\tan \left(\frac{\pi }{2}-\frac{\pi }{n}\right)=\cot \left(\frac{\pi }{n}\right).$$

Thus the plan decomposes into symmetric segments $x,x$ and $z,z$ and

$$\boxed{z=x\cdot \cot \left(\frac{\pi }{n}\right)}$$

(For a hexagon, $n=6$, this gives $\frac{z}{x}=\cot (\frac{\pi }{6})=\sqrt{3}$.)

Relating vertical and horizontal components

Now introduce the vertical component $y$ that corresponds to the slanted joist. In the vertical cross-section through a base vertex and the apex the joist forms the pitch angle $v$ with the base plane. Using the right triangle in that vertical section we have

$$\sin v=\frac{y}{x}⟹y=x\sin v,$$

where $x$ is the (appropriate) slanted/horizontal reference length introduced above and $y$ is the corresponding vertical rise.

The dihedral angle $\theta$ between the two symmetric facets can be related to the horizontal and vertical components: when you look in the bisector plane the half-angle $\frac{\theta }{2}$ satisfies

$$\tan \left(\frac{\theta }{2}\right)=\frac{z}{y}.$$

Substitute $z=x\cot (\frac{\pi }{n})$ and $y=x\sin v$ to eliminate $x$ and obtain

$$\tan \left(\frac{\theta }{2}\right)=\frac{\cot (\frac{\pi }{n})}{\sin v}$$

Final closed form

Solving for $\theta$ gives the compact general formula (valid for any regular $n$-gon base):

$$\boxed{\theta (v,n)=2\arctan \left(\frac{\cot (\frac{\pi }{n})}{\sin v}\right)=2\arctan \left(\frac{1}{\sin v\tan (\frac{\pi }{n})}\right)=2\arctan \left(\csc v\cdot \cot \left(\frac{\pi }{n}\right)\right)}$$

This expression connects the joist pitch $v$ and the polygon geometry (via $n$) to the dihedral ridge angle $\theta$.

The formula is compact, works for any regular $n$-gon, and cleanly reduces to the simple constants for square, hexagon, and other regular bases. It is directly useful for geometry problems as well as practical roof design calculations.

Checks and useful special cases

• Regular hexagon ($n=6$):

  $$\theta (v,6)=2\arctan \left(\frac{\sqrt{3}}{\sin v}\right)$$

• Square ($n=4$):

  $$\theta (v,4)=2\arctan \left(\frac{1}{\sin v}\right).$$

• Flat roof ($v=\frac{\pi }{2}$, facets lie in the base plane):

  $$\theta \left(\frac{\pi }{2},n\right)=2\arctan \left(\cot \left(\frac{\pi }{n}\right)\right)=\pi -\frac{2\pi }{n}$$

  i.e. the angle reduces to the interior angle of the base polygon at the vertex, as expected.

Inverse relation

If $\theta$ is known and the desired pitch $v$ is required,

$$\sin v=\frac{\cot \left(\frac{\pi }{n}\right)}{\tan \left(\frac{\theta }{2}\right)}⟹\boxed{v=\arcsin \left(\frac{\cot \left(\frac{\pi }{n}\right)}{\tan \left(\frac{\theta }{2}\right)}\right)}$$